Analytics Blog

The Last Statistical Significance Calculator You’ll Ever Need
![]() In case you missed it, there is another blog post that was published prior to this one that provides further context into what you’re about to read. You can definitely read this as a standalone, but it may be beneficial to read the other post if you’re looking for some more background.
In case you missed it, there is another blog post that was published prior to this one that provides further context into what you’re about to read. You can definitely read this as a standalone, but it may be beneficial to read the other post if you’re looking for some more background.
The A/B testing significance formula is confusing. I’ve been doing this for long enough to know that it rarely clicks for anyone right away. If you know R or Python, you can calculate significance with relative ease, however that has its own learning curve. Luckily, we live in the age where tools exist online to help you determine if your variation data is statistically significant.
There are many A/B testing statistical significance calculators online; some use t-tests, others binomial tests, and some even include the functionality to do both. We at Blast, for example, published a Revenue per Visitor Calculator that uses a nonparametric approach to calculate statistical significance to determine which variant has the highest revenue.
Since we started hosting that calculator, we’ve gotten a number of requests to build something that fits ALL A/B testing data and scenarios — this includes both continuous and conversion based metrics. In the last few months we’ve been developing and testing this new calculator against some of the other popular calculators out there, and we are finally ready to unveil it.
Statistics Can Be Difficult

Statistical significance can be confusing. With terms like p-value, confidence, power, and probably a dozen others, simply having data can seem like the easy part. As an analytics and marketing consulting firm, Blast gets a ton of questions regarding these things. When working with clients, we want to provide the most rigor in our deliverables, so statistics becomes a necessity.
Revenue per visitor (RPV) has been a big point of interest for many of our clients, so we created a statistical significance calculator that performed analysis on RPV data. As we worked through many of these optimization projects, we realized the value of having a significance calculator that can perform different significance analysis depending on the metric being used. Further, we acknowledge that for some of these metrics there is more than one statistical approach that is capable of providing reliable results, depending on the client interests.
“Statistical significance can be confusing. With terms like p-value, confidence, power, and probably a dozen others, simply having data can seem like the easy part.” Click & Tweet!
To meet the various needs, we decided to create a new, totally free statistical significance test calculator. So, without further ado, here is our new one-stop statistical significance calculator that will serve all of your A/B testing analysis needs!
This blog post will not only explain how our new statistical significance calculator works, but also what it’s doing. The calculator is equipped to handle two sample tests (a control and one variant), and will provide clear and concise results. With this blog post, I hope to remove some of the mystique that surrounds these statistical methods.
Binomial Testing
The first option in the significance calculator deals with binomial metrics, or in other words, metrics that teams often refer to as “rates.” Things like conversion rate statistical significance, bounce rate statistical significance, transaction rate statistical significance, and so on; really anything that either did or did not happen in some proportion.
“One common misconception is that binomial results should be based solely on P-value to determine significance.” Click & Tweet!
The binomial test uses the proportion of conversions from the control, and compares to the variation, just like any other significance calculator you may have encountered. To use this calculation your team will need to input total traffic and total conversion volume for each variation.
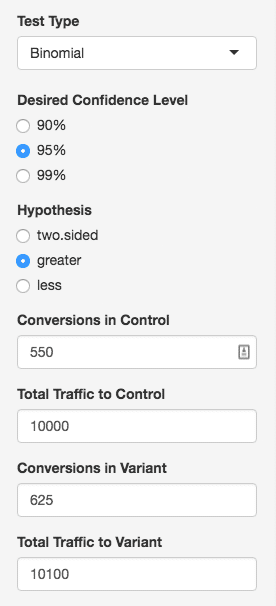
One common misconception is that binomial results should be based solely on p-value to determine significance. However, doing so lacks statistical rigor and if your team is following this approach, there is a real risk that your team will proceed with a change that won’t actually result in a positive impact. In addition to considering p-value, it is just as important to ensure results have the necessary level of power. The chart below outlines the differences between these two:
| Test Results | Reality | Probability of Happening | Logic |
| Impact Present | Impact Present | A | Statistical Power:A/(A+B) |
| No Impact | Impact Present | B | |
| Impact Present | No Impact | C | Statistical Significance (P-Value): C/(C+D) |
| No Impact | No Impact | D |
For example, if the original treatment has a 20% conversion rate that means users have a 20% probability of converting. If the variation is showing a 25% conversion rate, this doesn’t necessarily mean that your team is seeing a positive impact. What if in the control case, we had 10,000 visitors, and with the variant, we only had 100; with such a drastic difference in size between the two “samples,” we can’t really draw a good conclusion on whether the variation was actually better than the control.
This is where power comes in. Power is the inverse probability of rejecting something that should be true; a power of 80% (.8) will say that 20% of the time, things that should be detected, are not. If our variation is actually better than our control, a low power tells us that the test probably won’t pick up on that.
Using power, you can actually determine how large your variation sample should be so that you can be confident your results aren’t misleading you, or if you did use enough points (assuming you’ve already ran the test). Ideally a power of 0.8 or greater is desired.
Since it is important to account for power, you’ll see that the Blast Significance Calculator will display the power value in the results. Along with power, our test also displays relative lift, and of course, significance. Relative lift is defined as:
![]() (conversion rate of variation – conversion rate of control)/(conversion rate of control)
(conversion rate of variation – conversion rate of control)/(conversion rate of control)
And simply put, explains, in percentage form, how much one test is better than the other. As an example, using the rates above:
(.25 – .20)/(.2) = 25%
A relative lift of 25% sounds promising! However, the calculator makes it clear that the results are still not significant because our test was underpowered — our power is only .33.
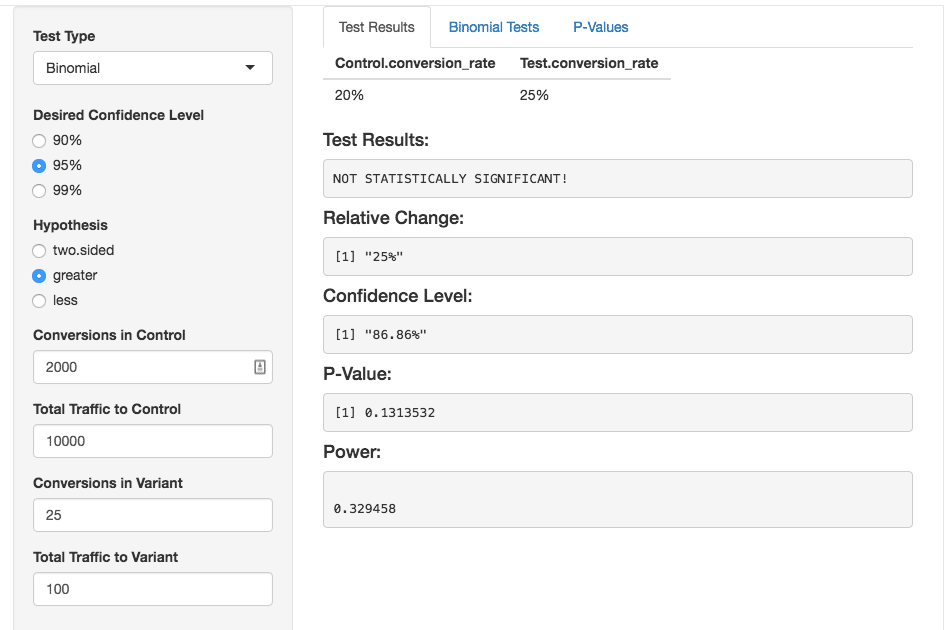
The calculator will not only tell you if your results are significant, but also all the key metrics like power and p-value.
This means that almost 70% of our positive results have a good chance of being interpreted incorrectly. You can still proceed; however, it’s not a great idea as there is much less integrity and rigor in your calculations. The best way to proceed is to use a sample size calculator prior to launching a test to determine the amount of visitors necessary for your test. This reduces the risk of your test results being underpowered.
Typically people test at a 95% significance threshold, meaning that for 95+ out of 100 tests, we see our variation being better than our control. The p-value is the inverse of that. You may hear that a p-value of .05 or less is desirable, and that essentially means the same thing as 95% confidence. If you need some more literature on it, you can view this page on p-values.
As an aside, the 95% level is widely used, but it is not something your team should blindly use. Every scenario is different, and you need to evaluate the level of risk you’re willing to accept. For example, if you need to be absolutely sure your two samples are different, a 99% confidence level is recommended, while faster moving teams may be okay with a 90% confidence level.
In the former case, you may need more data to reach significance at the 99% level, while in the latter, you can get by with less data but take on more risk. In either case, your data needs to have sufficient power, and we actually programmed the calculator to tell you not only when you have reached significance, but also if that significant result is of sufficient power to base a business decision.
Continuous Metrics

Continuous distributions can be thought of as data samples that contain many different numbers. Data that are considered to be continuous include (but are not limited to):
- Session-based metrics: average duration per session, pages per session
- User-based metrics: average order value per user, average revenue per user, average transactions per user, average pages per user
On our Statistical Significance Calculator, we provide two choices on how to deal with continuous data: parametric testing using a t-test, and non-parametric testing using a Mann Whitney test. I’ll spend some time on each of them.
Choice 1: Sampled T-Test Using “Average” Metrics
If your team is interested in looking at “average” metrics, such as average duration per session, average pages per session, or other aggregate measures, then you may want to consider using the t-test approach.
A t-test takes two samples (original and variant), and compares them to see if they’re drawn from the same big data set, called a population. You can perform a t-test with a small amount of data, but to be confident in the results, more data is always better (if you’re using e-commerce data, this shouldn’t be a problem).
“You can perform a t-test with a small amount of data, but to be confident in the results, more data is always better.” Click & Tweet!
Imagine we are testing height between two groups. Because we can’t test everyone in the world at all times, we take samples, maybe 50 people for our control, and 50 people for our variation. These two groups of 50 are our samples, and everyone in the world could be our control “population”.
When we compare our control and our variation samples, what we are figuring out is if they both came from the same human population, or maybe our variant is from an alien species. We hypothesize that these two samples are from different populations, and set out to test.
Because we did take the two groups from earth, our t-test “fails to reject the null hypothesis that the two groups are from different populations.” Because it was just a hypothesis, we don’t “accept” a hypothesis because it was just a thought we had and we only tested 100 people total, we just fail to reject it.
Now let’s put this into the context of a test on your website with two variations, the original and the variation. The population idea becomes a bit more abstract, but the implementation remains the same.
Let’s say that our control had 10,000 sessions, while the variation had 8,000 sessions. We can use our Statistical Significance Calculator to determine if the average session duration associated with the control is less than the average session duration associated with the variation. If the numbers are too close to tell, we probably fail to reject, but maybe when we test, we find that there is really good evidence that our variation is greater than our control; so much so, that we can be 95% confident that our variation average session duration is higher than our control average sessions duration.
This number is called our confidence, and the p-value is the inverse of this (.05 in this case). What the p-value says is the same thing, but worded differently; there is a small amount of evidence suggesting that these two samples are not from two different populations, but if it’s only 5% or so, then we are okay with that.
If that all sounds like a lot, and you just want to know “is the test statistically significant?”, we also provide a very clear printout at the top of the calculator that will let you know.
Sampling and the T-Test in Detail
The statistics behind a/b testing can be confusing, so I’ll talk about it at a high level briefly to hopefully shed some light on how to go about testing statistical significance. T-tests rely on parameters (mean and standard deviation) to compare our two samples. If you’ve seen a bell curve (called normal distributions), mean is the middle of it at the “average”, and standard deviation explains how spread out the data is.
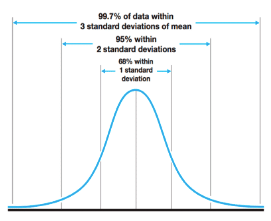
For some metrics, data isn’t spread evenly in this bell shape, so we can’t test it using the standard mean and standard deviation approach.
 However, there is a workaround, which applies a “sampling distribution” using the “Central Limit Theorem”. I would recommend this video for more of a thorough explanation of this approach.
However, there is a workaround, which applies a “sampling distribution” using the “Central Limit Theorem”. I would recommend this video for more of a thorough explanation of this approach.
To accommodate for this non-normal data, we can use aggregate metrics, like the “average”; so instead of pages views, we get average page views. If we have 10,000 points in our control group, we can “sample” a number of points. We then take the mean or average of this smaller group of points, and we get a “sample mean”.
We can do this a whole bunch of times until we have 30+ sample means for both the control and variation data samples. It’s important to understand, that really all we’re doing is taking a subset of points from each sample, and taking the average of them.
Example:
Base Samples:
Control: 5,6,7,8,9,10,11,20,5,4,2,25
Variation: 2,4,5,3,2,4,6,5,6,10
| Sample | Control | Sample Mean | Variation | Sample Mean |
| 1 | 2, 25, 11 | 12.67 | 6, 5, 5 | 5.33 |
| … | ||||
| 30 | 10, 11, 20 | 13.67 | 10, 2, 3 | 5 |
As you can see, we “sampled” 3 points from each base sample, and found the mean of the 3 points. We can do this 30 times, and we’ll end up with a “sampled” distribution of means. So even if our actual data doesn’t look like a bell curve initially, the samples do (so long as you take around 30 or more samples). We can then compare sampled distributions since they have a mean and standard deviation similar to that of a bell curve.
The takeaway here is that sampling data a whole lot of times will create a normal distribution for these metrics and as a result, it becomes possible for your team to measure statistical significance for the “average” of these metrics using a t-test. Specifically, you would need to use a t-test that allows you to enter user level or session level data.
You may be wondering why you can’t just use total conversion counts, and that has to do with the scope of the test. If you are only concerned with conversions, then that is definitely a good approach. However, continuous metrics aren’t as binary as yes or no, and they contain magnitudes like revenue or time on site. With these metrics, a t-test needs to take into account those magnitudes so that you can find the variation that has the greatest value, rather than the most conversions.
“The Blast Statistical Significance Calculator…takes the burden off users and still provides statistical rigor to the results.” Click & Tweet!
Now using a t-test for continuous metrics would normally create an additional burden for users; they would need to manually create the samples and calculate sample variances before analyzing for statistical significance. The Blast Statistical Significance Calculator implements a pooled variance approach, and uses the standard equation to calculate sample variance on the back-end. Doing so takes the burden off users and still provides statistical rigor to the results.
Choice 2: Non-Parametric Testing — All Points Considered
Our second approach for calculating significance for a continuous metric is meant for teams that know their data is not normally distributed and they want to use every data point for significance calculations. Specifically, the third selection on our calculator is the Non-Parametric calculator (the approach that is used for the RPV Calculator).
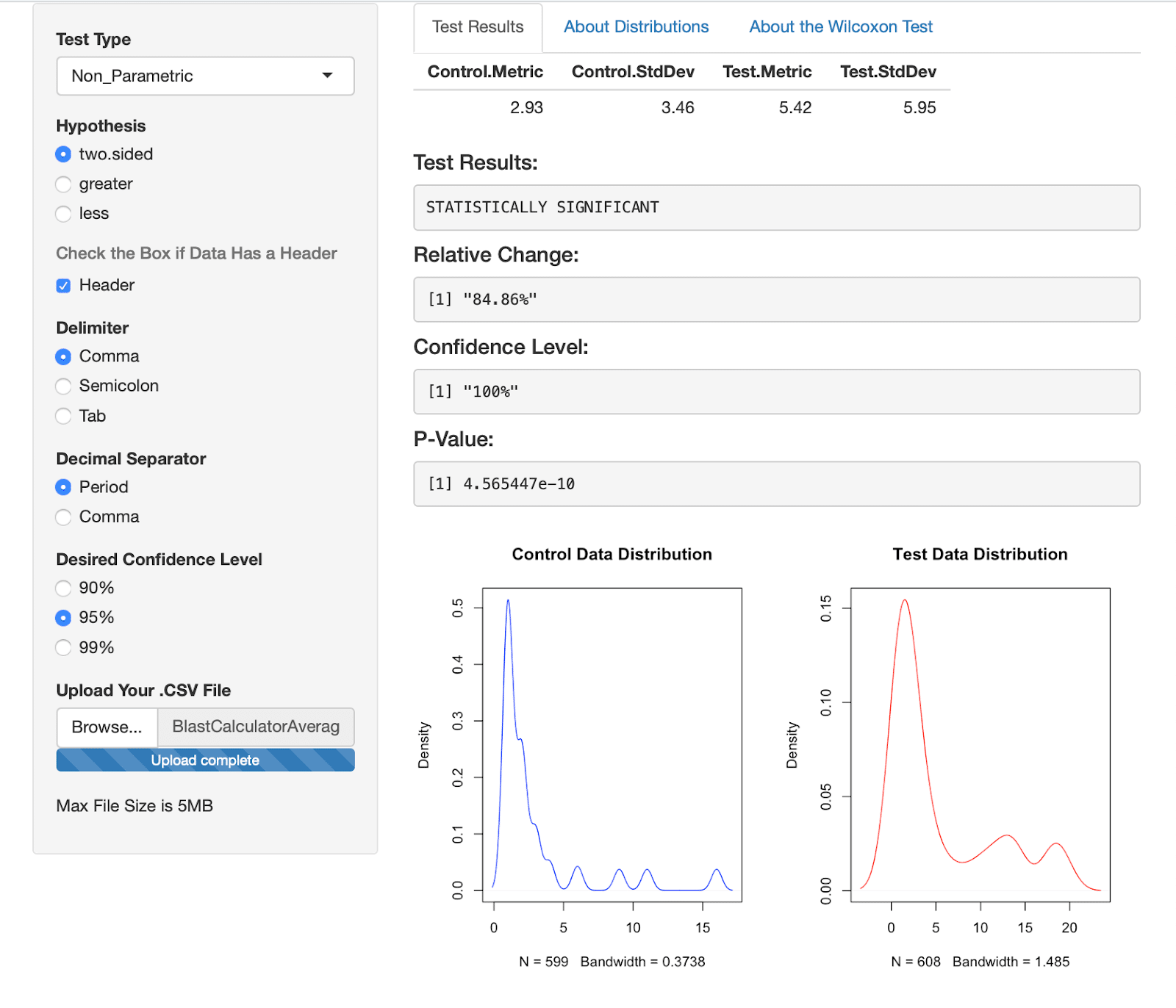
We have already written about this approach in a past blog post, but I’ll explain again here in lesser detail. Instead of using mean and standard deviation, a non-parametric test (the Mann-Whitney Wilcoxon in this case) compares each number of the Control sample to each number of the Variation sample and determines which sample is relatively larger. So every point in our control data sample would be ranked against every point in our variation data sample.
The methodology behind this can be summed up by “which variation is relatively larger?”, and it’s pretty straight forward.
Before moving on, I want to address a point of contention for statistical significance in the testing space. As mentioned previously, e-commerce data has a habit of being very skewed. There is nothing wrong with skewed data, but special care needs to be taken to run tests with it.
Which Continuous Testing Approach Should You Use?
“How do you determine statistical significance?” is a common question we get, and unfortunately there are many ways to calculate it. The two options we provide for continuous metrics in our new calculator are the main two approaches used in the industry, and each have their strengths and drawbacks.
On one hand, t-tests are more powerful and more likely to reach a sufficiently powerful statistical significance faster because it’s measuring the difference in sample means (or the averages), while non-parametric tests use ALL the data, and by default, are meant to handle non-parametric (skewed) data.
Normally, performing a t-test for continuous metrics would require extra effort for users since they would have to manually calculate the variance; however, as mentioned above, our calculator eliminates the need to do this because it does all of the variance calculations on the back-end.
As a result, the prep work needed for either approach (t-test or non-parametric test) is roughly the same. Most of the leg work will take place in setting up your analytics platform to track session-level data (ex. Session Id) or user-level data (ex. Client Id) and then ensuring your CSV is formatted properly.
Once this setup has been completed and you want to test, either approach is viable to use. That said, you should expect to get different results when using either the non-parametric or the parametric approach since they go about the calculation differently.
We encourage your team to determine which approach is right for your business needs, and use that calculation. We have provided all the tools to run either test, but we cannot make the final decision for you, as every use case is different.
The Calculator User Interface
If you have seen our Statistical Significance Calculator, you probably noticed there are many options in each of the testing interfaces.
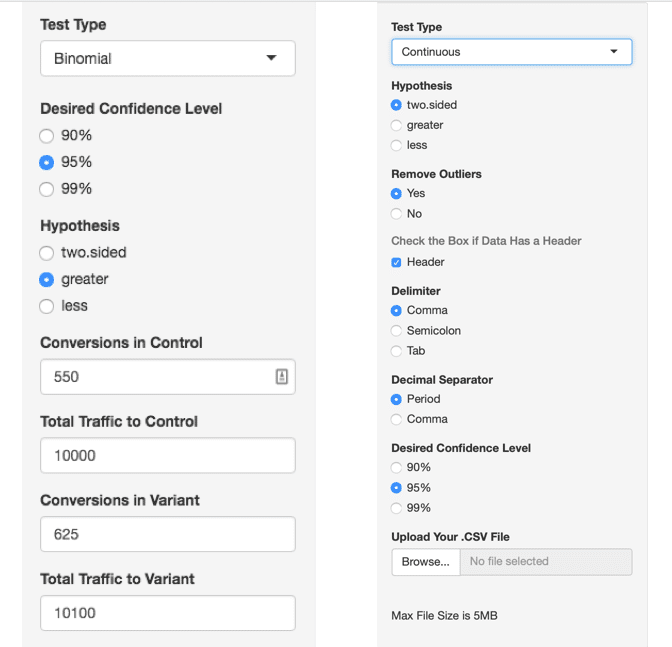
For Binomial testing, it’s as easy as entering your conversions and traffic for your control and test variation and then deciding what kind of test you want to perform, however there are many more when looking at the continuous metrics.
Most of the options have to do with the formatting of your CSV file. If you’re in America, the defaults should work fine. If you’re outside the U.S., you may need to adjust so that your decimal and delimiter are different (in America, decimals are ‘.’ and delimiters in CSV files are ‘,’ — other countries’ decimal and delimiter conventions may vary).
For the continuous t-test and non-parametric approaches, you’ll also see an option to upload your CSV file. The “Hypothesis” is all about how you want to compare your two data sets. If you want to check if the samples are different in any way, use “two-sided,” and if you want to test if the variation sample is greater or less than your control, use “greater” or “less” respectively to select that.
Lastly, including outliers (values that fall well outside the normal range) can be useful for some testing, but more often than not, you’ll want to remove outliers from your data. By default, our calculator will remove outliers, however this functionality can be turned off by selecting “No” under “Remove Outliers.”
Conclusion
While it was fun developing the new Blast Statistical Significance Calculator and this blog post, we didn’t do it just for kicks. This calculator was designed to not only provide a better user experience, but also to provide a ton of functionality by introducing the two new testing approaches.
Even though our calculator is a fully functioning product, that doesn’t mean we are going to stop improving it. The industry continues to EVOLVE and new methods are coming out all the time. As they’re tested and shown to be viable, we’ll be updating the calculator to reflect what the industry deems most reliable.
Thanks for reading! Definitely give the Blast Statistical Significance Calculator a try! After you’ve tried it, we’d love to get your feedback in the comments of this post.








